মৌলিক বিজ্ঞানের বিভিন্ন তত্ত্বের কথা বইতে আমরা সকলেই পড়েছি। কম সময়ে, কম মেহনতে বেশি উৎপাদন করার মতো প্রাথমিক চাহিদা থেকে দৈনন্দিন জীবনকে সহজ সুন্দর করে তোলা, সর্বত্রই তার প্রয়োগ। বিজ্ঞানের সে প্রয়োগের পরিসর থেকে খেলাধূলার জগতও বা বাদ থাকে কেন? সদ্য টোকিও গ্রীষ্মকালীন অলিম্পিক শেষ হয়েছে, আর তার সাথেই অতিমারির দরুন মনের যে করুণ দশা হয়েছিল, তাও খানিক কেটে গেছে। কারণ, স্বাধীনতার পর প্রথম ভারতীয় হিসেবে অ্যাথলেটিক্সে জ্যাভেলিন ছুঁড়ে সোনা জিতলেন পানিপথের নীরজ চোপড়া। প্যারালিম্পিক্সেও জ্যাভেলিন ছুঁড়ে দেশের হয়ে সোনা জিতেছেন সুমিত অন্তিল। জ্যাভেলিন বা গোদা বাংলায় আমরা যাকে বল্লম বা বর্শা বলি তা ছোঁড়ার পিছনের বিজ্ঞানই এই নিবন্ধের আলোচ্য বিষয়।

শুরুতেই বল্লমের বদলে বরং প্রাস (Projectile) নিয়ে আলোচনাটা শুরু করা যাক। কোনো বস্তুকে মাটি থেকে ছোঁড়ার সময় যদি তা অনুভূমিকের সাথে কোণ করে (Obliquely) ছোঁড়া হয়, আর তার ফলে বস্তুটি যদি বাঁকা (Curved) পথে চলতে থাকে, তাহলে তাকে আমরা প্রাসের গতি বলি। এই প্রাসের গতি সংক্রান্ত সব প্রশ্নের উত্তর পাওয়া যায় পদার্থবিজ্ঞানের একটি বিখ্যাত সূত্রকে কাজে লাগিয়ে – নিউটনের গতিসূত্র। 

১৬৬১ সালে স্যর আইজ্যাক নিউটন কেমব্রিজ বিশ্ববিদ্যালয়ের অধীনে একটি কলেজে পড়তে আসেন। এখন যেমন গোটা বিশ্বে করোনার প্রকোপ চলছে, তেমনই ১৬৬৫-র গ্রীষ্মে ইংল্যান্ডের শহরাঞ্চলে প্লেগ মহামারি ছড়িয়ে পরে। ‘লকডাউন’ শব্দটার তখন তেমন প্রচলন না থাকলেও রোগের প্রকোপ রুখতে সরকারি নির্দেশে সব কলেজ বন্ধ হয়ে গেল। ইংল্যাণ্ডের উলস্‌থর্প বলে একটি জায়গায় ছিল নিউটনের গ্রামের বাড়ি, তিনি সেখানেই ফিরে এসে বস্তুকণার গতি সংক্রান্ত বিষয়ে গবেষণা করতে থাকেন। এই গবেষণার ফলাফলই পরবর্তীকালে তাঁর লেখা বিখ্যাত বই প্রিন্সিপিয়া-তে (Philosophiae Naturalis Principia Mathematica) প্রকাশিত হয়েছিল। নিউটনের তিনটি গতিসূত্র আছে, তবে প্রাসের গতি বোঝার জন্য আমাদের দরকার দ্বিতীয়টি। এই সূত্রে নিউটন বলেছেন কোনো বস্তুর ওপর বল প্রয়োগ করলে কিভাবে তার গতির পরিবর্তন হয়। কোনো চলন্ত বস্তুর ওপর যে বল কাজ করছে, যদি তার পরিমাণ জানা থাকে, তাহলে এই গাণিতিক সূত্র ধরে দু-লাইন অঙ্ক কষলেই আমরা নিখুঁতভাবে বলে দিতে পারব বস্তুর গতিপথ (Trajectory) কেমন হবে। এই অঙ্কের সিদ্ধান্ত অনুযায়ী প্রাসের পাল্লা (Horizontal Range) মূলত দুটি জিনিসের ওপর নির্ভর করে: ক) কত জোরে বস্তুটিকে ছোঁড়া হচ্ছে অর্থাৎ ছোঁড়ার সময়কার গতিবেগ (Initial Velocity), এবং খ) অনুভূমিকের সাথে কত কোণ (Initial Throw Angle) করে ছোঁড়া হচ্ছে। এখন যদি এমন হয়, যেখান থেকে বর্শা ছোঁড়া হচ্ছে (Launching Point) আর সেটি যেখানে গিয়ে পৌঁছচ্ছে (Landing Point) দুটোই মাটি থেকে একই উচ্চতায় আছে, তাহলে তার সমাধান অপেক্ষাকৃত সহজ। কিন্তু অ্যাথলেটিক্সে বল্লম ছোঁড়ার সময় খেলোয়াড় তার উচ্চতা অনুযায়ী মাটির খানিকটা উঁচু থেকেই বল্লমটি ছোঁড়েন। এরপর বল্লমের ডগা যেখানে মাটি ছোঁয়, সেই দূরত্বকে ওই খেলোয়াড়ের বল্লমের পাল্লা হিসেবে ধরা হয়। আমাদের নীরজের ক্ষেত্রে এটা ছিল প্রায় ৮৭.৫৮ মিটার। তাহলে প্রাসের আলোচনায় গ) কোন উচ্চতা থেকে সেটাকে ছোঁড়া হচ্ছে (Initial Throw Height) তাও গুরুত্বপূর্ণ। আবার এমন নয় যে অলিম্পিকের ময়দানে কোনো বাতাস ছিল না! ফলে পাল্লা নির্ণয়ের অঙ্কটা আরও শক্ত হয়ে যায়। বাতাস কোনদিক থেকে কত বেগে বইছে তার ওপরও পাল্লা নির্ভর করে। সেসব নিয়ে বিশদে চর্চা করার জন্য পদার্থবিজ্ঞানের একটি শাখা তৈরি হয়েছে - বায়ুগতিবিদ্যা (Aerodynamics)। খাটুনি কমানোর জন্য ধরে নেওয়া যেতে পারে বাতাস না থাকলে প্রাসের পাল্লা যা হওয়া উচিত, বাতাসের বাধা থাকায় সেটা একটু কমে যাবে। 

এখন অঙ্কটা কষার সময় ধরে নেওয়া হল প্রাসটি ছোঁড়া হয়েছে মোটামুটি ৫ ফুট ১০ ইঞ্চি উচ্চতা থেকে অনুভূমিকের সাথে ৪৫ ডিগ্রি কোণ করে। ৩টি আলাদা প্রাথমিক বেগের জন্য প্রাসের পাল্লা কী হবে ১ নং ছকে তা দেখানো হল -    

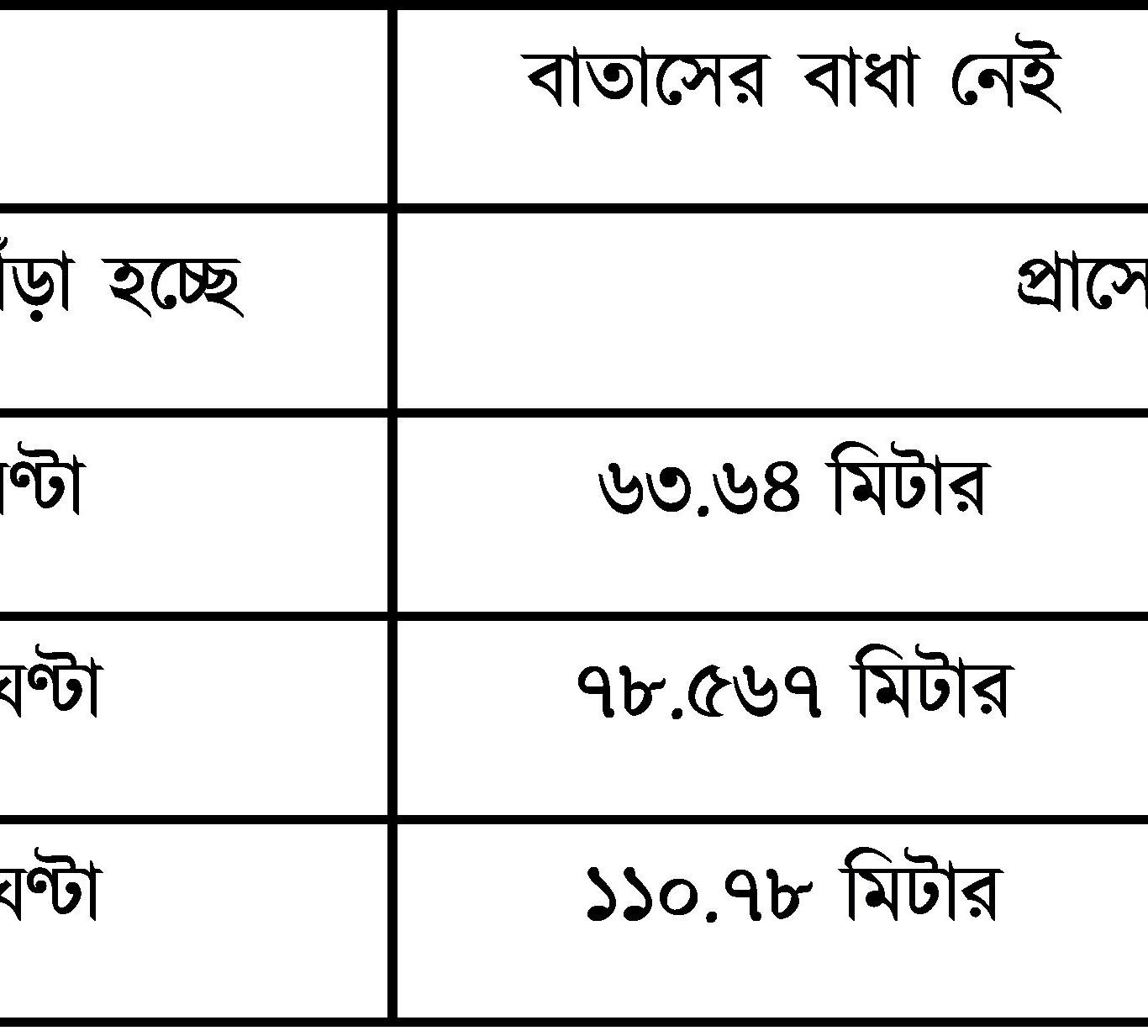
(৩টি আলাদা প্রাথমিক বেগের জন্য প্রাসের পাল্লা)

অর্থাৎ, যত বেশি জোরে ছোঁড়া হবে, বল্লম তত দূরে গিয়ে পড়বে। 

এবার একটা অন্য প্রসঙ্গে আসা যাক। ধরা যাক, প্রাসটিকে আগের মত উচ্চতা থেকেই ঘণ্টায় ১০৮ কি.মি. বেগে ছোঁড়া হল। তাহলে কোন কোণে প্রাস ছোঁড়া হলে পাল্লা কত হবে সেটা ২ নং ছকে ব্যাখ্যা করা হয়েছে -   

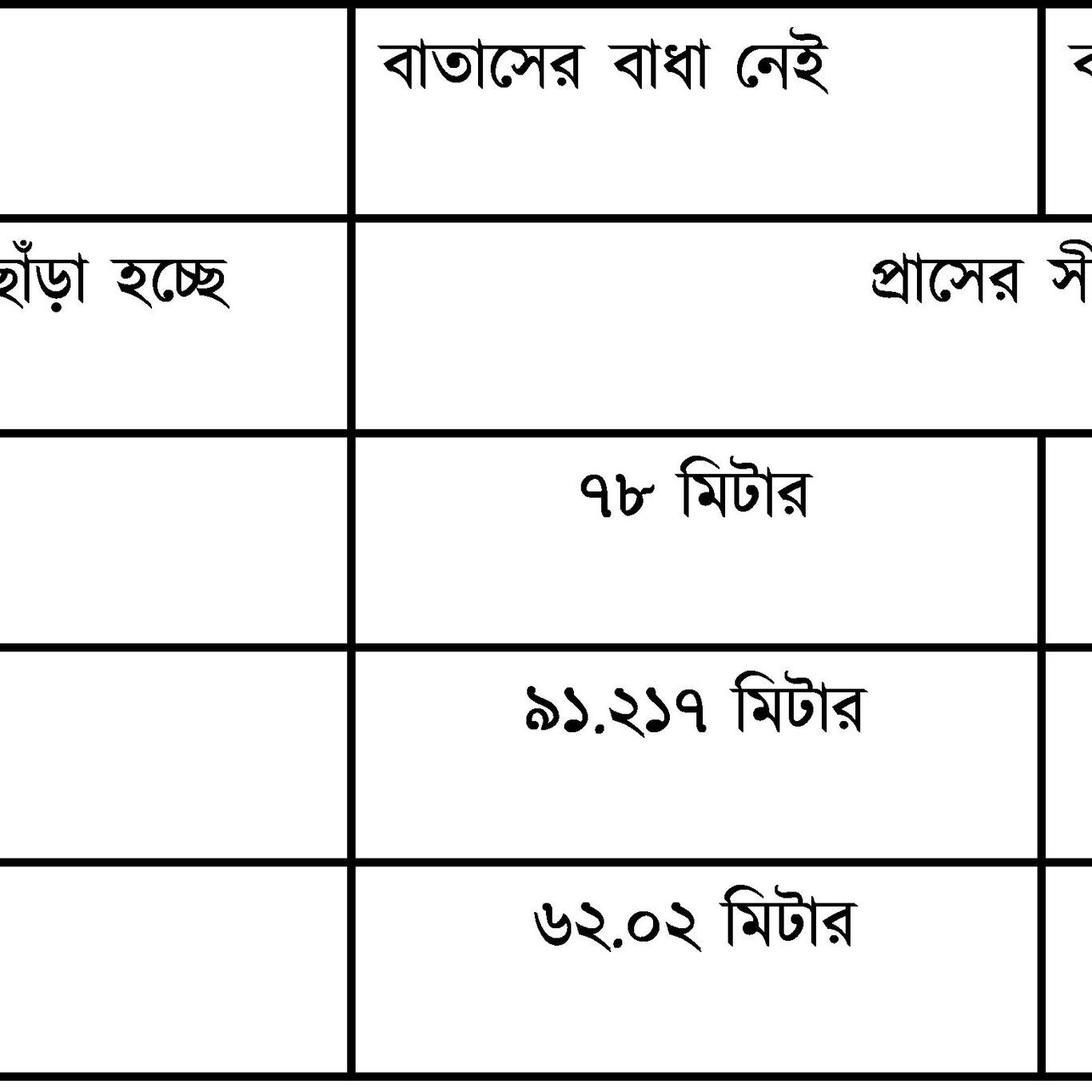
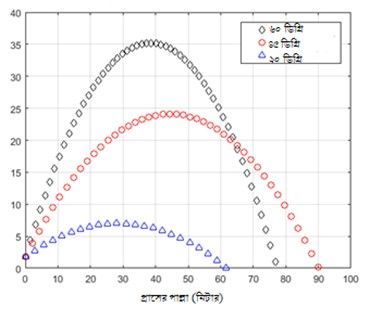
(৩টি আলাদা প্রাথমিক প্রক্ষেপ কোণের জন্য প্রাসের পাল্লা)

তার মানে ৪৫ ডিগ্রি হল এমন উপযুক্ত কোণ যাতে প্রাসের পাল্লা সবচেয়ে বেশি হয়। তার চেয়ে কমবেশি হলেই পাল্লা কমে যাবে। 

আবার যদি ধরে নিই প্রাসটি যখন অনুভূমিকের সাথে ৪৫ ডিগ্রি কোণ করে ছোঁড়া হয়েছিল তখন তার প্রাথমিক গতিবেগ ছিলো ১০৮ কি.মি. প্রতি ঘণ্টা, তাহলে দুটি ভিন্ন উচ্চতার ক্ষেত্রে প্রাসের পাল্লার মাপ ৩ নং ছকে লেখা হয়েছে -  

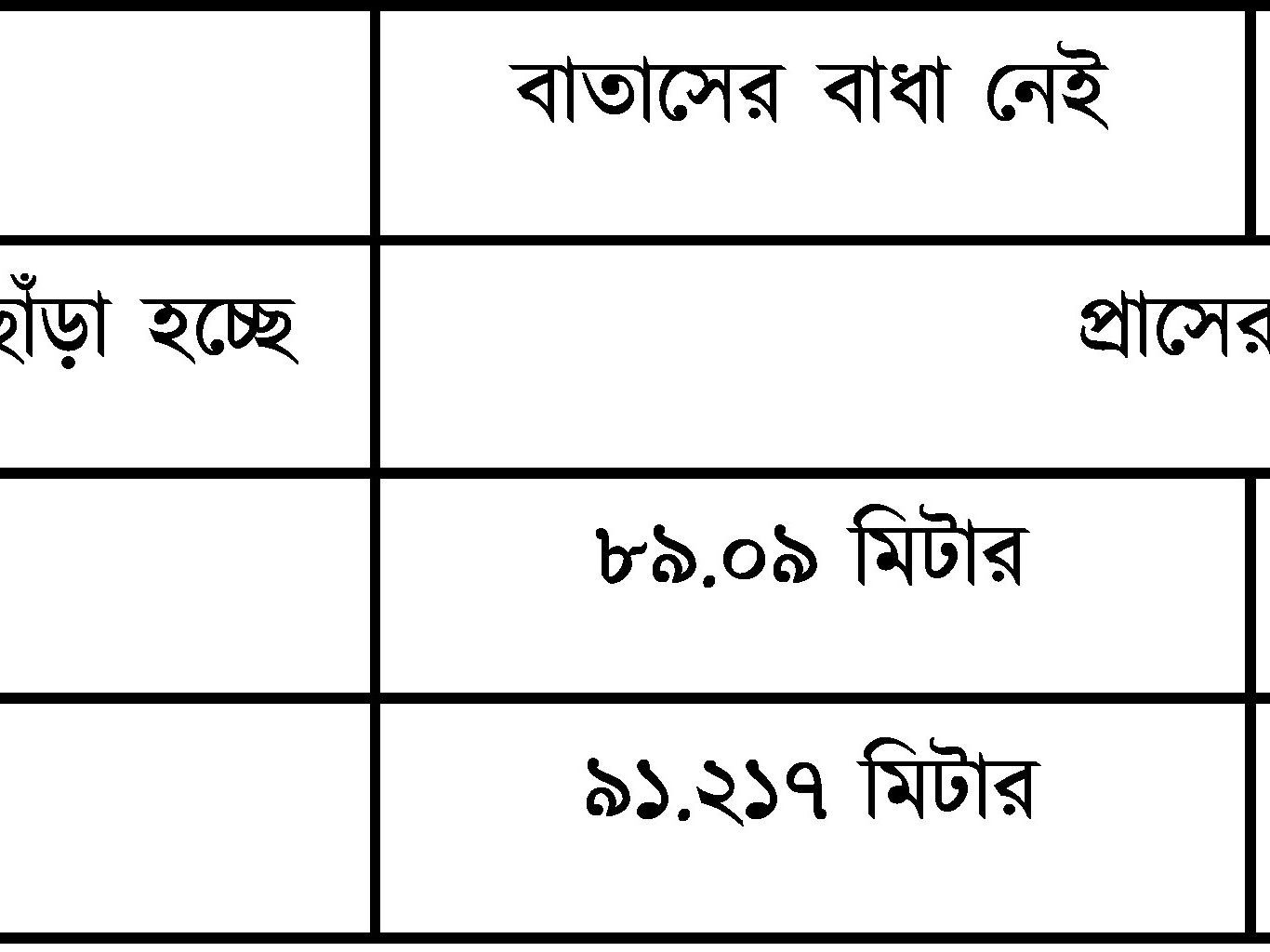
অর্থাৎ, দেখা যাচ্ছে ৪ ফুটের চেয়ে ফুট চারেক বেশি উচ্চতা থেকে একই বেগে একই কোণে প্রাস ছুঁড়লে তার পাল্লা প্রায় ২ মিটার বেড়ে যাবে। 

তা বলে এমন নয় যে প্রাসকে বেশি দূরে ছুঁড়তে গেলে তাকে বেশি উচ্চতা থেকেই ছুঁড়তে হবে। কম উচ্চতা থেকে ছুঁড়েও একই পাল্লা পাওয়া যায় যদি ছোঁড়ার গতিবেগ বাড়ানো যায় কিংবা প্রক্ষেপ কোণ পালটানো হয়।  

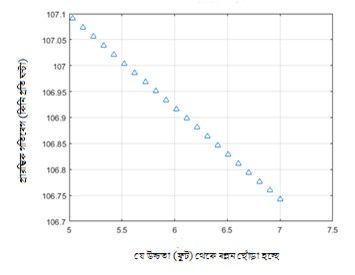
(প্রাস নিক্ষেপের উচ্চতা ও গতিবেগের পারস্পরিক নির্ভরতা)

ধরা যাক কেউ ৭ ফুট উচ্চতা থেকে একটা প্রাস ৪৫ ডিগ্রি কোণে ১০৬.৭৪২২ কি.মি. প্রতি ঘণ্টা গতিবেগে ছুঁড়ল। অঙ্ক বলছে এর সীমা হবে ৯০ মিটার। এখন ঐ প্রাসটিকেই যদি ৫ ফুট উচ্চতা থেকে ছোঁড়া হয়, তবে একই সীমা পেতে বেগের মান বাড়িয়ে ঘন্টায় ১০৭.০৯৬৭ কি.মি. (উপরের ছবি) করতে হবে। মানে আরও জোরে ছুঁড়তে হবে। এখানে মনে হতেই পারে পাল্লার এত কম পার্থক্য নিয়ে মাথা ঘামানোর কারণ কি? কারণ অলিম্পিক প্রতিযোগিতায় কয়েক মিলিমিটারের তফাতে পদক হাতছাড়া হয়ে যায়। 

প্রাস সংক্রান্ত যে গণনা আমরা করলাম, এইবার তাকে প্রয়োগ করা যাক বল্লম ছোঁড়ার ক্ষেত্রে। প্রথমেই আমাদের মাথায় রাখতে হবে বল্লম বা অ্যাথলিট কেউই একটা বস্তুকণা নয়, অনেকগুলো বস্তুকণার সমবায়ে গড়া একটি বিস্তৃত দৃঢ় বস্তু (Extended Rigid Body)। তাই ছোঁড়ার সময় যখন অ্যাথলিট বল্লমের ওপর বল প্রয়োগ করেন, তখন গোটা বল্লমের ওপর প্রযুক্ত বলের প্রভাব হিসেব করা মুশকিল হয়ে দাঁড়ায়। কিন্তু, যদি ধরে নেওয়া হয় যে বল্লমের সমস্ত বস্তুকণার ভর সংকুচিত হয়ে তার ভরকেন্দ্রে (Centre of Mass) জমা আছে, তাহলে গোটা বল্লমের গতিটাকে শুধুমাত্র তার ভরকেন্দ্রের গতি হিসেবে ভাবা যাবে। অ্যাথলিটের গতির ক্ষেত্রেও একই নিয়ম খাটবে। অলিম্পিকে দেখা যায় সাধারণত অ্যাথলিটরা ঘন্টায় প্রায় ২০ কি.মি. বেগে ছুটে এসে বল্লম ছোঁড়েন। ছোঁড়ার সময় অ্যাথলিট তার শরীরের সমস্ত শক্তি কাঁধ হয়ে কনুইয়ের মাধ্যমে বল্লমে পাঠান। মাটিতে দাঁড়িয়ে থাকা কোনো পর্যবেক্ষকের সাপেক্ষে, ঠিক ছোঁড়ার মুহূর্তে, বল্লমের ভরকেন্দ্রের গতিবেগ দুটো জিনিসের ওপর নির্ভর করে: ক) সেই মুহূর্তে অ্যাথলিটের ভরকেন্দ্রের গতিবেগ, আর খ) অ্যাথলিটের কব্জির গতিবেগ। এই দুই বেগের যোগফল (Resultant) থেকে বল্লমের প্রাথমিক বেগ চূড়ান্তভাবে নির্ণয় করা যায়। বেগের যেহেতু মান ও দিক দুইই আছে তাই এই যোগ ভেক্টর সংযোজনের নিয়ম অনুযায়ী হয়। 

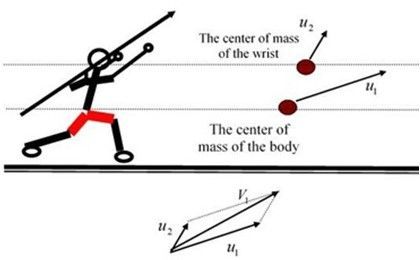
(ঠিক বল্লম ছোঁড়ার সময় অ্যাথলিটের ভরকেন্দ্রের বেগ আর কব্জির ভরকেন্দ্রের বেগের লব্ধি)

এ তো গেল বোঝানোর সুবিধের জন্য সহজ একটা তুলনা। কিন্তু আসল বল্লম ছোঁড়ার সময় আরও অনেকগুলো বিষয় বল্লমের পাল্লাকে প্রভাবিত করে। যেমন বল্লমের মাপ, গঠন, রঙ করার পর সব জায়গা সমান মসৃণ কিনা, ইত্যাদি। এই সব কিছু ধরে অঙ্ক কষতে গেলে আধুনিক কম্পিউটারের সাহায্য নিতে হয়। মুম্বইয়ের টাটা ইনস্টিটিউট অব ফান্ডামেন্টাল রিসার্চ-এর বিজ্ঞানী ডঃ অর্ণব ভট্টাচার্য সবকিছু নিয়ে হিসেব করে দেখিয়েছেন মাটি থেকে প্রায় ৩৬ ডিগ্রি কোণ করে বল্লম ছুঁড়লে তুলনামূলকভাবে সবচেয়ে সন্তোষজনক ফল পাওয়া যায়। 

সুতরাং দেখা যাচ্ছে গতিসূত্রকে কাজে লাগিয়ে সূক্ষ্ম মাপজোখ করলে একজন অ্যাথলিট নিঁখুত ধারণা পেতে পারেন কিভাবে ছুঁড়লে বল্লম সবচেয়ে বেশি দূরে গিয়ে পড়বে। নিউটন নিজে হয়ত ভাবতেই পারেননি তার সূত্রের এমন প্রয়োগ হতে পারে! অথচ তাঁর পরিশ্রমলব্ধ ফসল দেখিয়ে দিচ্ছে, অ্যাথলিটের শুধু পেশির জোর থাকলেই চলবে না; শক্তির সাথে তাল মিলিয়ে ছোঁড়ার কৌশলও শেখা চাই। সেই অনুযায়ী অনুশীলন চললে তবেই সাফল্য আসবে। তাই সরকারি স্তরে মৌলিক বিজ্ঞানের গবেষণাকে ক্রমাগত উৎসাহিত করা প্রয়োজন। তাতে রাতারাতি তেলের দাম কমবে না ঠিকই, কিন্তু ভবিষ্যতের পাথেয় গড়ে উঠবে। 

**************************

[গাণিতিক গণনা করার সময় ধরে নেওয়া হয়েছে: পৃথিবীর অভিকর্ষ ত্বরণের মান S.I. এককে ১০; বাতাসের বাধা প্রাসের গতিবেগের তাৎক্ষণিক মানের সাথে সমানুপাতিক (FAir ∝ v); আপেক্ষিক সমানুপাতিক ধ্রুবকের মান S.I. এককে ০.০০৬।

প্রচ্ছদে ও লেখায় ব্যবহৃত সমস্ত ছবি লেখকের সূত্রে প্রাপ্ত।]

**************************

তথ্যসূত্র: 

(১) https://www.facebook.com/ratul196/posts/3960796094026572

(২) www. duniyaadaari.com

(৩) https://doi.org/10.31459/turkjkin.516625  

(৪) https://twitter.com/TifrArnab/status/1424235490715176965