গত কয়েকমাসে বিজ্ঞানীমহল থেকে চা-কাকু, গোঁসা ব্যুরোক্র্যাট থেকে ছা-পোষা চাকুরে, সোনালী চুলের মহামহিম থেকে নমোস্য বাজিগর – হক্কলের মুখে মুখে ফিরছে ‘flatten the curve, flatten the curve’। কার curve? কিসের curve? তাকে flat-ই বা করবো কেন? দিব্যি ঝলমলে টলটলে একটা curve-কে গুঁতিয়ে জিরো সাইজ করে দেওয়ার জন্য কেন এতো উদ্বেগ? তবে স্যোশাল নেটওয়ার্কিং- এর মতো গণ-শিক্ষাব্যবস্থার অভূতপূর্ব অভ্যুত্থানে এইসব আবালখিল্যি বিষয়ে লেকচার এখন আর পাবলিক শোনেনা, সে এখন লেকচার দেয়। বিজ্ঞান আর বুদ্ধির বাজারদর এখন মোবাইল কোম্পানির রিচার্জ প্ল্যানের সমান। জাতি-ধর্ম-উদ্দেশ্য-আগ্রহ নির্বিশেষে এই জ্ঞানের প্রসার আসলে জনমানসে বুদ্ধিবৃত্তির সর্বজনীন প্যামফ্লেট বিতরণের সমান। ফলত, এখন আর প্রচারের ভস্মে পয়সা খরচ করে ঘি ঢালতে হয়না।

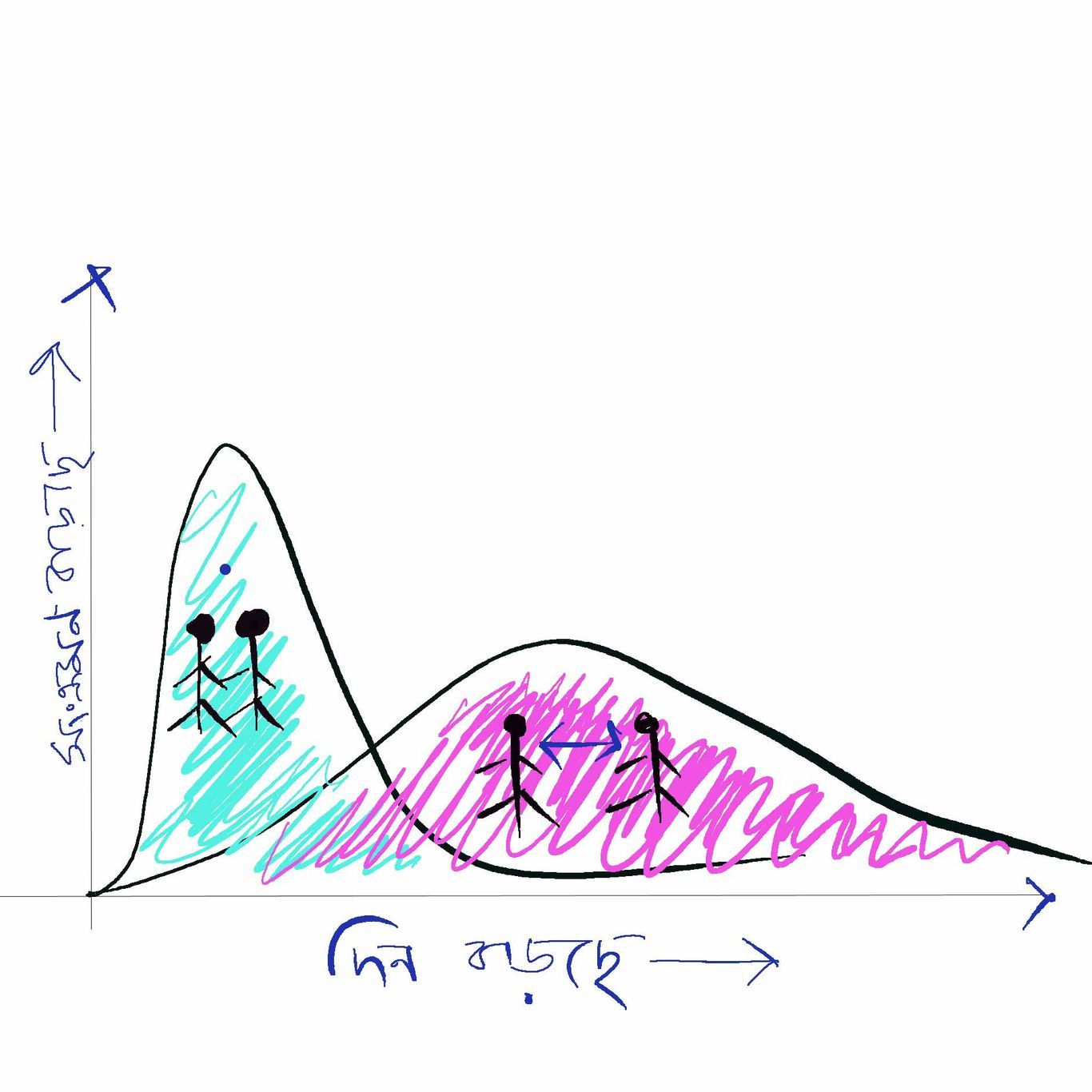
যাই হোক, ‘Flatten the curve’ বিষয়ে সাধারণ জ্ঞান খানিকটা এরকম – করোনা নামক হঠকারী ভাইরাসটি যখন প্রতিনিয়ত চেষ্টা করবে হাজারে হাজারে নতুন কলোনির গোড়াপত্তন করতে, পাবলিকের কাজ হবে সেই চেষ্টাকে প্রতিরোধ করে সংক্রমণের সময়কে কিছুটা দীর্ঘায়িত করা যাতে সরকারি চিকিৎসাব্যবস্থা পরিষেবা দেওয়ার ন্যূনতম সময়টুকু পায়। প্রতিরোধের পদ্ধতিও অজানা নয়। গলায়-গলায় ভাব, আহ্লাদি-আশনাই ইত্যাদি সম্প্রসারিত ভাব বিনিময় ব্যতিরেকে স্যোশাল ডিস্ট্যান্সিং বজায় রাখা, স্বাস্থ্য সম্পর্কে অর্বাচীনতা ভুলে সভ্য হওয়া, সচেতন হওয়া ইত্যাদি। এ হল ওষুধপত্র ছাড়া বিবিধ সামাজিক পদ্ধতি অবলম্বন করে প্রতিরোধ গড়ে তোলার উপায়, non-pharmaceutical interventions নামেই পরিচিত। গত মার্চে WHO-এর Centre for Infectious Disease Modelling এবং আরও কিছু আন্তর্জাতিক বন্ধু গবেষণাকেন্দ্র, কোভিডের সংক্রমণ curve-কে flat করার জন্য non-pharmaceutical interventions-এর ব্যবহার সংক্রান্ত একটি বিস্তারিত গবেষণাপত্র প্রকাশ করে। সেখানে লক-ডাউনের উপর বিশেষ জোর দেওয়া হয়। এছাড়া এতদিনে জনমানসেও এই বিষয়ে নিজস্ব মতামত তৈরী হয়েছে। তবুও কিশলয় স্তরের কিছু ধারণা ঠিক পরিষ্কার হয়না; যেমন, কীভাবে সংক্রমণের curve পাওয়া যাবে, পেলেও তাকে চেপেচুপে বসিয়ে দেওয়ার আশু প্রাপ্তি কী, বা এই চেপে দেওয়ার রাজনীতিতে কে বা কাদের প্রত্যক্ষ বা পরোক্ষ হাত রয়েছে ইত্যাদি ইত্যাদি। ভনিতা ছেড়ে পরিমার্জন করলে মূলত তিনটি প্রশ্ন দাঁড়ায় - এক, সংক্রমণের ধরন কিরকম? দুই, ভবিষ্যতে এই ধরন কতটা পাল্টাবে বা আদৌ পাল্টাবে কিনা? আর তিন, কোন্‌‌ কোন্‌ বিষয়ের উপর সংক্রমণের বিস্তৃতি নির্ভরশীল? এই তিনটি বিষয় পরিষ্কার হলেই সংক্রমণ রোখার বিকল্প পরিসর ছকে ফেলা সম্ভব, কেবলমাত্র সামাজিক অভ্যাসের ঈষৎ অদলবদল ঘটিয়ে, যেমনটা ইদানীং ঘটাবার চেষ্টা চলছে বিশ্বব্যাপী। এই বিষয়ক আলোচনাই Epidemic Modelling-এর ভিত্তি-উদ্দেশ্য-প্রাণ। এই বিষয়ের চর্চা, মানে রোগের ক্ষয়ক্ষতি সম্পর্কে আগেভাগেই ধারণা তৈরী করে সেই নিয়ে জনমানসে সচেতনতা গড়ে তোলার প্রথম পদক্ষেপ, প্রায় ৩৫০ বছর আগে John Graunt রচিত একটি রিপোর্ট ‘Natural and political observations made upon the bills of mortality’। এই রিপোর্টে মৃত্যুর কারণের ভিত্তিতে, সপ্তদশ শতকে ব্রিটেনে মৃত ব্যক্তিদের মোট ৮১ টি ভিন্ন গোষ্ঠীতে অন্তর্ভুক্ত করা হয়। তবে কোনো মহামারীর সংক্রমণকে গাণিতিক মডেলের সাহায্যে প্রকাশ করার প্রথম কাজটি করেন Daniel Barnouli, ১৭৬০ সালে, ফ্রান্সে স্মলপক্সের সংক্রমণ বিষয়ে। সহজ করে বললে, কোন রোগের বিস্তার যে বিষয়গুলির উপর নির্ভর করে (যেমন- বিশেষ ভাইরাসটি কতটা ছোঁয়াচে, সেটা জলবাহিত না বায়ুবাহিত, সংক্রমিত স্থানের জনঘনত্ব কিরকম, ইত্যাদি) সেগুলিকে একটা সমীকরণের মধ্যে নিয়ে আসা। ধরা যাক, ‘a’ বাড়লে সংক্রমণ দ্রুত ছড়ায় আর ‘b’ বাড়লে সংক্রমণ হ্রাস পায়। স্কুল বয়েসে অঙ্কে যারা সর্বৈব ফাঁকি মেরেছে, তারা ছাড়া সবাই বুঝতে পারছি, এই সংক্রমণ বিস্তারের হারকে ‘a/b’-এর সমানুপাতিক বলা চলে। এই সমীকরণটাই সংক্রমণের সহজ Mathematical Model। তবে Epidemic Modelling-এর যে গাণিতিক ভাবনাটি বহুল প্রচলিত, তার আবির্ভাবকাল ১৯২৭, Kermack আর Mckendrick-এর হাত ধরে। মনে করা যাক, এক বা একের বেশি সংক্রামিত ব্যাক্তিকে (Infected - I) একটা জনগোষ্ঠীর মধ্যে ছেড়ে দেওয়া হল যেখানে সকলের মধ্যেই সেই রোগের সংক্রমণ হতে পারে, অর্থাৎ প্রত্যেকেই Susceptible (S)। রোগটি যেহেতু ছোঁয়াচে, তাই একজন I এর সংস্পর্শে একজন S এলেই রোগ সংক্রমণের সম্ভাবনা থাকবে। যত সংক্রমণ বাড়বে, তত ঐ নির্দিষ্ট জনগোষ্ঠীর S-সংখ্যা কমতে থাকবে এবং I-সংখ্যা বাড়বে। কিন্তু সংক্রামিত যারা, তাদের মধ্যে কেউ কেউ তো সুস্থও হবে (Recoverd - R), আবার কেউ মারাও যাবে। সুতরাং I-সংখ্যাও একসময় কমতে থাকবে। অন্যদিকে S-সংখ্যাও যে শুধুই কমতে থাকবে তাও নয়, কারণ সবাই যে I-এর সংস্পর্শে আসবে তার কোন মানে নেই, বিশেষ করে ঐ গোষ্ঠীর জনসংখ্যা যদি অনেক বেশি হয়। তবে জনসংখ্যা কত হলে সংক্রমণ কত হবে, I কতদিন অব্দি বাড়বে, কত হারে বাড়বে, যখন কমবে তা একেবারেই কমবে নাকি আবার ফিরে আসার সম্ভাবনা রয়েছে - এসবই নির্ভর করছে হাতে-থাকা জনগোষ্ঠী ও রোগ সংক্রান্ত তথ্য এবং modelling কতটা নির্ভুল তার উপর। নিজেদের আর্টিকেলের শুরুতেই Kermack আর Mckendrick এই ভাবনাটিকে সহজ করে ব্যাখ্যা করেছেন। এই মডেলে উপরোক্ত তিনটি গোষ্ঠীরই জনসংখ্যা সময়ের সাথে পাল্টায়। কিভাবে পাল্টাবে, কতটা পাল্টাবে এসব নির্ভর করবে S কি হারে I-তে, বা I কত হারে R-এ পরিণত হয় তার উপর। যেমন, S-এর সংক্রমণ নির্ভর করে S কি হারে I এর সংস্পর্শে আসে (ধরি ‘a’) বা সংস্পর্শে এলেও সংক্রমণের সম্ভাবনা (ধরি ‘b’) কত, কারণ সব সংস্পর্শই তো আর গলায়-গলায় সোহাগ বা গায়ে হেঁচে দেওয়া নয়। আবার আমরা আগেই দেখেছি, S এর সংক্রমণের হার a ও b দুইয়ের যৌথ সমানুপাত। কিন্তু a স্বাভাবিকের চেয়ে কম হবে যদি লক-ডাউন থাকে। কতটা কম, সেটা নির্ভর করছে লক-ডাউন কতটা জোরালো তার উপর। লক-ডাউন চলছে, আর মনটা গামছা গায়ে দিয়ে পাড়ার মোড়ে দাঁড়িয়ে চা খাবার জন্য মিহি অভিমান করছে, তাহলে কি আর a কমবে! তবে এটুকু বোঝা যাচ্ছে যে a-এর মান বাড়িয়ে কমিয়ে লক-ডাউন, এমন কী স্বাস্থ্যসচেতনতাকেও আমরা model করতে পারি। ধরা যাক, কোনো আহাম্মক I আপনার সাথে করমর্দন করল বা হাঁচল আপনার গায়ে - অবশ্যই b এর মান বেশি হবে। এবার যদি আপনি সচেতন হন, সেই হাত সাবান দিয়ে ধুয়ে নেন, অথবা যে হাঁচল তার মুখে যদি মাস্ক থাকে তাহলে b নিশ্চিত কম হবে। যদি a ও b দুইই বেশি হয়, অর্থাৎ মানুষে-মানুষে খুল্লামখুল্লা মেলামেশাও বহাল তবিয়তে চলছে আর সচেতনতারও গ্রহণদশা, তাহলে খুব দ্রুত I- সংখ্যা বাড়বে, আর সময়ের সাথে সংক্রমণের একটা ঢ্যাঙা curve পাওয়া যাবে। এবার যদি হেব্বি জোরালো লক-ডাউন হয় (যা আর ত্রিসীমানাতেও দেখা যাচ্ছে না) আর স্বাস্থ্য সম্পর্কেও একটা গুরুগম্ভীর সচেতনতা আসে, তবে a ও b দুইই কমবে, সংক্রমণের লয় হ্রাস পাবে এবং curve মাটিতে বুক পেতে দেবে। শুধুমাত্র a ও b কমিয়ে বাড়িয়ে curve-কে ঠিক কতটা flat করব, বা যতটা flat করা কাঙ্ক্ষিত তার জন্য a, b ঠিক কী মানের হবে, এই দু’টি হল Epidemic Modelling-এর উপপাদ্য। তবে গাণিতিক মডেল থেকে সংক্রমণের সম্ভাব্য গতিপ্রকৃতি নিয়ে যে তথ্য পাওয়া যাবে, তাকে ভবিষ্যদ্বাণী বলে ভেবে নেওয়া ঠিক নয়। একে বরং সতর্কবার্তা হিসেবে নিলে সরকার বা সংশ্লিষ্ট কর্তৃপক্ষের লাভ, সেক্ষেত্রে প্রস্তুতি নেওয়ার একটা যথাযথ দিকনির্দেশ পাওয়া যায় এবং সকাল-বিকেল নিত্যনতুন পলিসি তৈরির দিগ্‌ভ্রান্তি থেকে নিষ্কৃতিও মেলে।

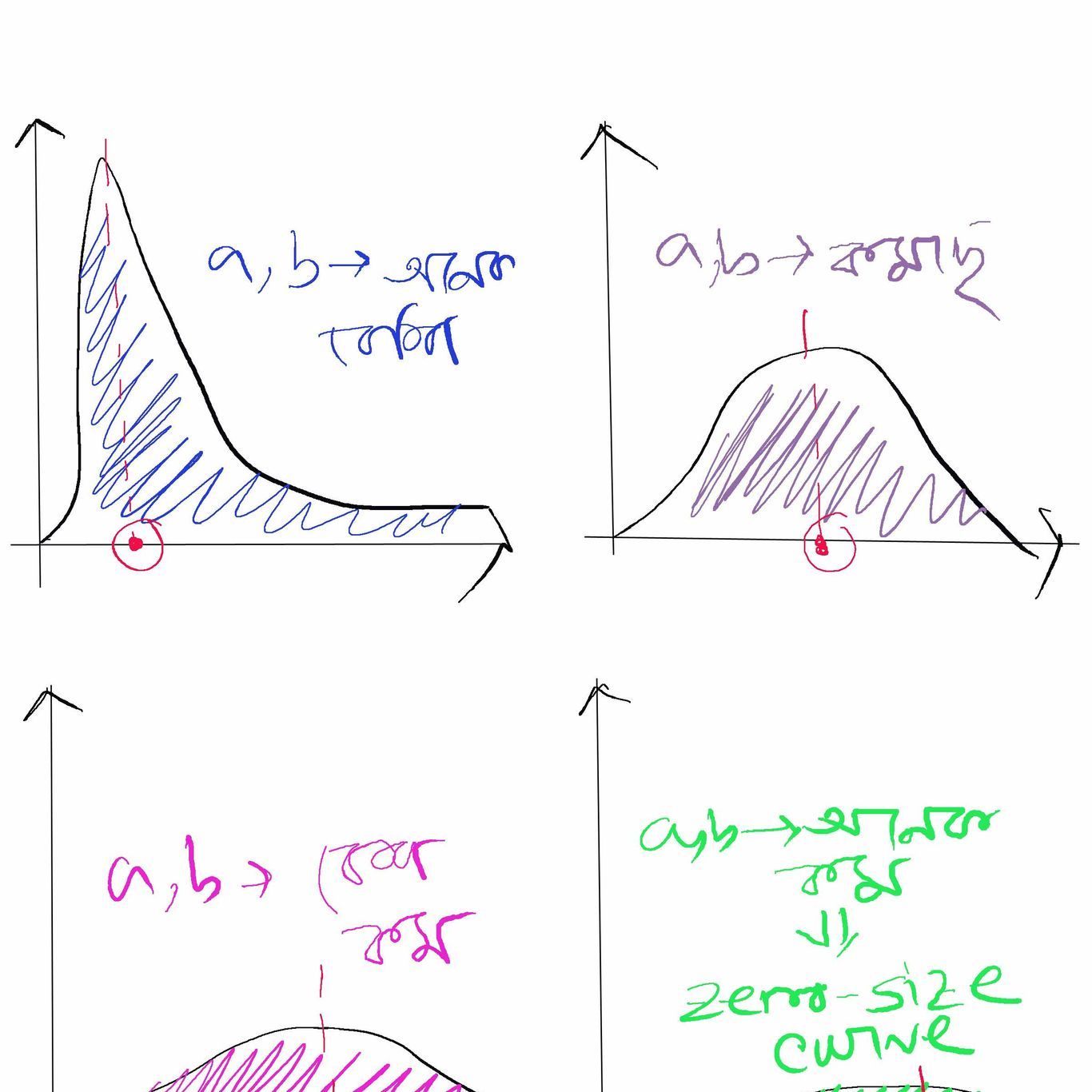
Karmek-Mckendrick model-কে আরও বাস্তবসম্মত করা সম্ভব যদি মোট জনসংখ্যাকে শুধু S, I, R-এর বদলে আরও বেশী গোষ্ঠীতে ভাগ করা যায়। যদি শুধু বর্তমান পরিস্থিতির কথা ভাবি, তাহলেও যারা সংক্রামিত (I), কেবল রোগের লক্ষণপ্রকাশের উপর ভিত্তি করেই তাদের আরও দু’ভাগে ভাগ করা যায়- symptomatic (লক্ষণযুক্ত) ও asymptomatic (লক্ষণমুক্ত) – যাদের থেকে সংক্রমণের সম্ভাবনাও (b) ভিন্ন। Asymptomatic শ্রেণীর শনাক্তকরণ মুশকিল, তাই এদের সংস্পর্শে আসার সম্ভাবনা বেশি, যদিও সংক্রমণের সম্ভাবনা তুলনায় কম। Symptomatic- দের ঠাঁই মূলত হসপিটালে। কিন্তু মোট আক্রান্তের তুলনায় যদি অনেক কম লোক সুস্থ হয় তাহলে স্বভাবতই সরকার হসপিটাল পরিষেবা দিতেও ব্যর্থ হবে। তাই সংক্রমণ curve-কে flat করা গেলে আর সেই সঙ্গে হসপিটালে বেডের সংখ্যাও বাড়ানো গেলে, R-সংখ্যা বাড়বে ও মৃত্যুহার কমবে। হসপিটালের বেড, আক্রান্ত রোগীর মৃত্যু, symptomatic ও asymptomatic-এর সংক্রমণের হার - সবকিছুর জন্যই মডেলে আলাদা আলাদা গোষ্ঠী/সূচক যুক্ত করা প্রয়োজন। Karmeck- Mckendrick model-এর মূল সুরটাকে বজায় রেখে মহামারীর চরিত্র ও জনগোষ্ঠীর বৈচিত্র্য অনুযায়ী তার যথাযথ পরিমার্জনই epidemiologist-দের কাছে প্রকৃত চ্যালেঞ্জ।

বছর দুয়েক আগে কেরালাতে নিপা ভাইরাসের সংক্রমণ মনে আছে নিশ্চয়ই, যা শিরোনামে এসেছিল তৎকালীন কেরালা সরকারের সংক্রমণ-প্রতিরোধী তৎপরতার জন্য। যে ভাইরাসের কবলে ২০০১-এ শিলিগুড়িতে ৪৫ জনের মৃত্যু হয়, কেরালায় সেই সংখ্যা ১৮। Gujarat University-এর একদল গবেষক বাদুড় থেকে মানুষে নিপা ভাইরাসের এই সংক্রমণকে গাণিতিক মডেলের সাহায্যে ব্যাখ্যা করেন এবং সংক্রমণ নিয়ন্ত্রণের পথও বাতলান। আমেরিকায় গবেষণারত দুই বাঙালী গবেষক তাদের মডেলে ব্যাখ্যা করে ভ্যাকসিন দেওয়া বা না-দেওয়ার ফারাকে কিভাবে একজন নিপা-আক্রান্ত বার্ধক্যে এনসেফালাইটিসের শিকার হতে পারেন। এছাড়াও বাংলাদেশের খুলনা বিশ্ববিদ্যালয়ের গবেষকরা মারণ ভাইরাসের সংক্রমণে ব্যক্তিগত পর্যায়ে স্বাস্থ্যসচেতনতার প্রভাব ব্যাখ্যা করতে modelling-এরই সাহায্য নিয়েছেন। University of New South Wales-এর গবেষক Tim Churches-এর করোনা সংক্রান্ত মডেলেও স্বাস্থ্যসচেতনতার গুরুত্বপূর্ণ প্রভাব আলোচিত হয়েছে। IISc-এর গবেষকরাও Epidemic Model ব্যবহার করে করোনা সংক্রমণের হারের উপর জন-ঘনত্ব, আক্রান্তের বয়স, লক-ডাউনের সময়কাল ইত্যাদির প্রভাব বিস্তারিত আলোচনা করেছেন। মহামারীর সময় Epidemic Modelling থেকে কী কী বোঝা যেতে পারে তাই নিয়ে এত যে ভনিতা করলাম, তা আসলে এটাই বোঝাবার জন্য যে আপৎকালীন পরিস্থিতিতে স্বাস্থ্যনীতি প্রণয়নের ক্ষেত্রে Epidemic Modelling নিঃসন্দেহে ফেলু মিত্তিরের থার্ড-আই হতে পারে। কোন নির্দিষ্ট জনগোষ্ঠীর মধ্যে সংক্রমণ কীভাবে ও কত দ্রুত ছড়িয়ে পড়বে, কী পদক্ষেপ নিলে পরিষেবা দেওয়ার যথেষ্ট সময় পাওয়া যাবে, সংক্রমণের হার কখন সর্বাধিক হবে, এই সমস্ত বিষয়ে সংশ্লিষ্ট কর্তৃপক্ষ (বিশেষত নির্বাচিত সরকার) মহামারী বিশেষজ্ঞদের পরামর্শ নিতেই পারে; এতে সংক্রমণের গতিপ্রকৃতি অনেক নিশ্চিতভাবে নির্ণয় করা সম্ভব। তবে কর্তৃপক্ষকে নিঃসন্দেহে শিক্ষিত ও দূরদর্শী হতে হবে, একরোখা নিধিরাম সর্দারদের কপালে কেবল বিধির কৃপাণ লেখা আছে।

তথ্যসূত্র :
১) Epidemic Modelling: An introduction (D.J. Daley, J. Gani)
২) Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and
healthcare demand (Imperial college COVID-19 response team)
৩) A contribution to the mathematical theory of epidemics (W.O. Kermack, A.G.
McKendrick)
৪) Simulating COVID-19 interventions with R (Tim Churches)
৫) Google, Google, Google!

[ ছবি ঋণ : The Statesman ]